Regression Analysis

Part 1

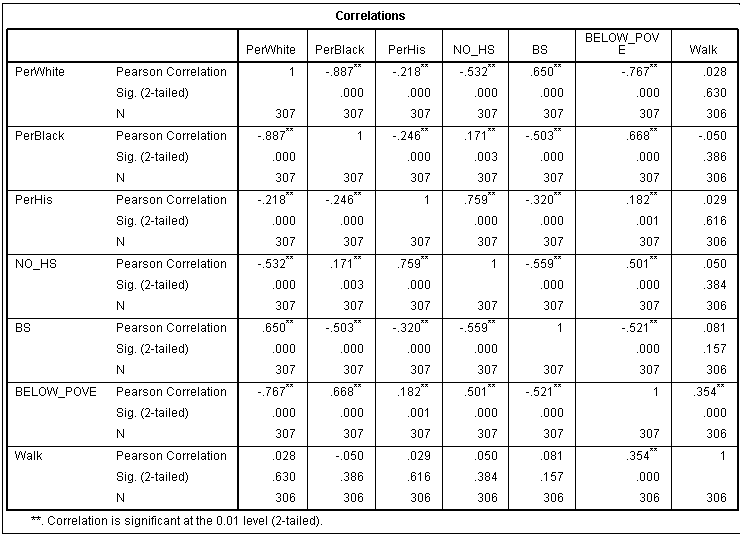
A study done on an unknown town is trying to test to the relationship between the amount of students who get free and reduced lunch and crime rates.  A news station within this town has made the claim that as the amount of kids who are receiving free lunch goes up, so does the crime rate.  Using the same 44 observations as the news station, a regression analyses will be ran to test if the percentage of persons enrolled in free lunch programs correlates too a differentiation in crime rates.  The null hypotheses in this instance would be that there is no relationship between percent of students receiving free lunch and the crime rate within Town X.

Using SPSS to run the regression analyses, the charts in figure 1 were produced.  The chart on the bottom, titled coefficients, eludes that there is some degree of linear association between the two variables based off of the significant value of .005, which falls outside of the confidence interval of .05. Also, the B value is 1.685 which indicates that the linear relationship is positive. Subsequently, the top chart, titled Model Summary, provides the R square value which describes the strength of causation between percent students receiving free lunch and crime rates.  This value provides what is known as the coefficient of determination, and in this case the value is .173.  In conclusion, we acknowledge that there is weak linear association, and therefor we reject the null hypotheses

Figure 1: charts displaying results of linear regression analyses ran in SPSS.

Using linear regression equation, what percentage of persons will get free lunch with a crime rate or 79.7?

y = a + bx

independent variable = percent free lunch
dependent variable = crime rate

a= constant  (shown in coefficients chart)
b= regression coefficient
y= 79.7%
x=?

79.7= 21.819 + 1.685 (x)
x= 34.35%


Part 2: Introduction 

Using the college enrollment data from all 72 counties in the state of Wisconsin, the University of Wisconsin state school system wants know why students chose the schools that they ultimately end up attending.  Does the overall trend show students going to schools close by? faraway? Or does the county distance from a school not matter and socio-economic factors like education and household income have more of an effect.  It must be acknowledged that there are many unknown variables which can not be accounted for in this analyses, the goal is simply to see if particular variables will display any correlating trends.  The data that we have for each county is: % population with a Bachelors degree, median house hold income, and the distance from each county's center to the different UW schools.  The schools being used to test the null hypotheses, that there is no linear relationship between distance, % population with a bachelors degree, median house hold income, and the number of people attended, are  UW Eau Claire or UW Parkside.

Methods

To find out if any of these factors are significant, a series of regression analyses were conducted to test the relationship between the number of graduates from each school per county and the factors alluded too in the intro.  A total of six linear regressions were ran, all of which had either UWEC students or UWPS graduates per county as the the constant dependent variable and pop/distance, median household income, or percent population with a Bachelors Degree as the independent variable.   Conducting linear regression indicated if any and what variables affect the amount of students from each county attend the schools in question. 

Of these six regression analyses ran, only three were found to be significant based on a one tale test with a 95% confidence interval.  So the only results that will be discussed from here forth will be those that fell outside of the 95% range, since they rejected the null hypotheses.

The linear regression that yielded significant results were:

1. population of UWEC students per county compared too population/distance
2. population of UWEC students per county compared too percent population of county with BS degree
3. population of UWPS students per county compared too population/distance

Note: population of students per school in each school was normalized by distance so the counties with large populations don't create false data.  The counties that contain the states larger cities cities likely have the most students enrolled all over the state school system, hence why the normalization of distance is necessary.

Results

1. Results of Regression analyses between population UWEC students to population/distance per County.

The linear relationship between distance and population of students per county poses very high coefficients of determination.  This not only concludes the linear nation of relationship, but it is strong enough that it can be a tool to help predict the future enrollment patterns based off of a counties distance from UWEC.  The overall pattern of the residual range suggest that the closer ones county is to the campus, the higher likelihood they will attend the UWEC. Looking at the map one can see that there is significant clustering of higher residual categories around Eau Claire County.  The other counties that exhibit high portions of UWEC studetns are those that reside on the eastern side of the state where a large portion of the states population lives.  The fact that these areas still demonstrate high residual values despite  being on the other side of the state suggest that there is a motive at play here that isnt quite as tangable or obvious.  Perhaps its showing a body of students that want to escape the big cities and see what life is like an a more rural/town environment



2. Resaults of regression analyses between population UWEC students and Percent of counties population with a BS Degree.

 When analyzing the relationship between UWEC students and percent BS degrees per county county is that there is not a very strong coefficient of determination.  Despite the fact that there is a linear relationship between the two variables, the low coefficient determination would indicate that the presence of higher or lower % BS degrees per county has little affect on the amount of students from that county that attend UWEC.  Another way this variable could be applied to show stronger relationship is to apply the same variable to the entire network of Wisconsin state schools.  This would test the assumption that a college education for ones children is more common if they come from a family or environment where a college education is more common. 

3. Results of regression analyses between population of UWPS students percounty and population/distance per county

Similar to the comparison between UW Eau Claire and distance, the comparison between UW Parkside students and population/distance per county also showed a high coefficient of determination.   The predictive value of the relationship is especially significant when one looks at the map and can clearly see that not many people attend UWPS who are not from the eastern or south eastern part of the state.   Another observation that can clearly be seen is that the highest residual degree is only associated with two counties; the county the school is in (Kenosha) and the county directly north of Kenosha County (Recine). Of all the results discussed, the findings in this analyses show the highest degree of predictive value.

Conclusion 

running regression analyses to see what factors contributed to how many people per county go to a certain school yielded some interesting results.  The main finding was that the distance between UWEC/UWPS and a given county is a huge factor in predicting where a student will go to university. Personally, i can say that this factor did way into my decision greatly, I dint want to leave too far from home, but i wanted to be far enough away where i want tempted to go home all the time.  With that being said, I'm sure many students weigh many other variables when deciding what school to attend, and some universities tend to attract more people from closer locations than others.  In light of my results, smaller schools, like UW Park-side, and to a smaller degree, UWEC, would be able to use the results of this analyses to sharpen the focus of their advertising and recruitment to the counties that immediately surround them.

Correlation and Spatial Autocorrelation Lab

Part 1: Correlation 

For the introductory portion of this lab, students ran correlation analyses on a data set to test the relationship between distance (ft) and sound level (db).  The null hypotheses in this case would be that here is no linear relationship between the distance from the source, and how strong the sound is  To test the null hypotheses,  the data was analyzed in excel and SPSS to get both the direction and strength of the relationship. The data was used in Excel to create a scatter plot with a trend line, which was used to provide the direction of the correlation.  The minimum values of the x an y values were adjusted so the data better filled out the graph area.  As the graph indicates, there is a negative correlation where as distance increases, the sound level decreases (figure 1).  The next operation was too find the strength of association between these two variables, which was done using the 'bi-variate correlation' tool in SPSS.  The resulting r value of -.896  in this operation indicates that there is a strong association between distance and sound level. As a result, we reject the Null hypotheses that there is no linear correlation.

figure 1

figure 2 

Part 2: Creating and Analyzing a Correlation Matrix.


Looking at the correlation matrix for the 307 census tracks in Milwaukee County, one can see a range of correlations pertaining to the racial demographics, education, and socio-economic factors within the county.  The trend that is displayed in these correlations paints a general picture of segregation and inequality. To exemplify this overall trend within the county, it is important to pay attention to the observable correlation between the variables presented in figure 3 below.  The first correlation that shows a degree of segregation is shown in the strong-negative correlation between percent black people/census track and percent white people/census track (-.887).  Subsequently, there is a strong positive correlation between percent black people/census track and percent below poverty level/ track (.668).  When looking at the same comparison for white people though, you see the opposite trend of a strong negative correlation correlation (-.767).   These three correlations previously commented on indicate that on track to track basis, that if there is a high percent of white people in the track, there is a high probability of there being a low percentage of black people and a low percentage of people below the poverty line.

figure 3

Part 3: Spatial Autocorrelation - Introduction 

For this section, the TEC is asking to find any patterns in voting demographics for elections that occurred in 1980 within the state of Texas.  The data you have been given for these two election periods is the overall voter turnout and the percent of the democratic vote, per county.  subsequent to this electoral data, data was also downloaded that contained the total population of Hispanics per Texas County in 2010.  The goal is to report back if voting patterns have changed in the past 20 years; and if so, how?  The null hypotheses that we are testing is if there is no change in voting patterns between 1980 and 2008, and the alternative hypotheses being that there is a difference between in voting trends between these two years.


Methods

Spatial Auto correlation is a tool that is used if one is trying to see how a single variable changes over a given area if the data is in a continuous format.  Following Tobler's first law of geography, that things closer together are more related and interconnected than things further away, spatial auto correlation than allows one to create a much more useful concise statistical picture of how a variable undergoes variation over a given space.  Most other statistical methods are based on the assumption that the values of observations in each observation, occur independent of one another. Spatial autocorreltaion allows you to see what areas show clusters where there are significantly high values of your variable, clusters of significantly low, and areas where there are hi values surrounded by low, or low values surrounded by hi.


The value used to measure of the degree of autocorrelation in this study is Moran's I.  Moran's I is applied to the zones or point where the autocorrelation is being conducted, and provides you with a number between -1 to 1.  The closer Moran's I is to 1, the more clustered the the the data is.  The direction (+/-) tells you if there is clustering (+) or if there isn't (-).

To visually comprehend how the spatial distribution of Hispanic populations and democratic voters, LISA auto-correlation maps were created to show areas of Texas where clustering is occurring, where it is not, and where out-lier counties are.  In order to create these maps, a spatial weight must be created within Opengeoda.  The spatial weight that was created was based off of shared border length. as a result,   Larger counties which had more a large boarder perimeter, and a large amount of smaller counties around it were given a heavier weight than smaller counties.  This addition of a spatial weight to the auto correlation provides a spatial element that helps create areas of clustered similarities.

To produce these values and maps, all data and weights were created/inputted into in OpenGeoda, a free interface for geo-statistical analyses. the correlation matrix produced was created in SPSS.



Results and Subsequent Conclusions 

• High - High = counties that show a high level of the variable, and are surrounded by other counties which exhibit high levels of the variable 
• Low-Low = counties that show a low level of the variable and are surrounded by other counties which exhibit low levels of the variable 
• Low - High = counties that exhibit a low level of the variable but are near areas that show a high level of the variable 
• High - Low = counties that show high levels of variables but are near areas that show low levels of the variable

Percent of population of Hispanics per County in Texas, 2010

This map illustrates the highest degree of spatial autocorrelation out of all the observations.   Along the border with mexico, there is distinctly visible high-high clustering, and a high degree of low-low clustering in the Eastern part of the state.  besides a select few high-low or low-high outliers, The general trend suggests that Hispanic populations are more concentrated near the Mexican border in the south/south western part of the state, and moves toward low-low levels of clustering as you move north and east. In addition to the visual prevalence of the clustering, the subsequent Moran's I of .78 further suggest a high degree of positive autocorrelation.



Percent Democratic voter turnout (2008 top - 1980 bottom)

Between the years of 1980 and 2008, the voting pattern of percent democratic voters become more clustered and less random.  where there was once counties of 'high-high' democratic vote percentage in 1980, there isn't in in 2008.   The maps would suggest that for some reason the democratic vote shifted from pockets in the south/south east to being more concentrated near the border areas in the south/south west, and a small part of the north east.  Subsequently, the Moran's I value increased between these two years from 0.58 to .7, further indicating that a higher degree of clustering is occurring of percent democratic vote turnout per for each county in Texas.


Voter turnout (2008 top - 1980 bottom) 



































Unlike the spatial auto correlation conducted on percent democratic vote between the two years 1980 and 2008, the spatial auto correlation of overall voter turnout between 1980 and 2008 showed a decrease in the amount of clustering; the Moran's I score drooped from .46 in 1980 to .36 in 2008.  The clustering that is still occurring, however, has shifted from the south west of the state up toward the middle, north and north eastern parts of the state.  Subsequently the, southern tip of the state that was almost entirely high-high, is now entirely low-low.  The reason for this switch could be any number of factors; growth of population in new areas, the decrease of population in other areas.


To further investigate if there are any correlations between the variables that occurred in the same year (2008), a correlation matrix was produced in SPSS.  Since it would make no sense to analyze the correlation of things that occurred 28 years apart, the correlation focused on the comparing percent Hispanic population per county, and the 2008 % democratic vote and overall voter turn out per county.  what can be seen is a moderately strong negative correlation between % Hispanic population and voter turnout but see a moderate strong correlation between % Hispanic population and % democratic turnout. The later observation indicates that as the % of democratic voters increases through out the state, there is a significant probability that you will find a higher % of a counties population being Hispanic.  Transversely, the moderately strong negative correlation between % Hispanic population and overall voter turnout suggests a higher probability of counties that have a low voter turnout also having a high percentage of the population being Hispanic.

Report to the TEC 

In conclusion to the reports and maps created, the Null hypotheses would be rejected in this scenario because a large spatial shift in voter turnout and % democratic vote can be observed across counties within the state of Texas between 1980 and 2008. Reporting to the Governor, the findings from this report would suggest that the spatial distribution of voting patterns have changed from 1980 to 2008.  The southern part of the state which in 1980 exhibited an area with a predominantly low voter turnout made a complete change to 2008, and became an area of high voter turnout.  one possible reasoning for this could be related to the high Hispanic population that we now see there in the 2010 data.  With more time and resources, analyzing the Hispanic populations within the state around the time of the 1980 election would allow for a more in depth analyses of the possible influence of Hispanic population on the overall voter turn out within the state of Texas.  In terms of the % democratic vote, the shift of clustering toward the southwestern part of the state coincides well with the % Hispanic population clustering exhibited in 2010.  At this point in time, Hispanics largely vote democratic, so this trend isn't particularly alarming. The governor now should be better able to comprise a plan of action of where to focus his campaign  efforts to reach the parts of the state with the highest voter turnout and while also targeting clusters of Hispanic populations.

Significance and Chi-Squared Testing

Part 1

*note: for the ‘z/t value’ section, the +/- indicator implies that the critical value is both above and below the mean (o) point.  The values that do not have +/- in front of it will only have one critical value, and could be either in the + range or – range, but not both.

2. The data presented to us in this problem is trying to test if there is a difference between the populations of three Invasive insects in Buck County in comparison to estimated population numbers per field in the entire county.  The null hypotheses is that there is no difference between the invasive species population in the 50 fields sampled from Buck county, and estimated values.  The alternative hypotheses is that there is a difference in these populations.     After calculating the Z scores of the sampled bug populations from the 50 selected fields and comparing their placement in comparison to the 1.96 or -1.96 critical value which was derived from using a two tailed test with 95% confidence, it was concluded upon that null hypotheses for each set of insect data should be rejected.  In conclusion, the insect population for the sampled 50 fields in Buck County for some reason or another have elements that cause there to be more Asian-Long Horned Beatles               (z= 2.47)and Emerald Ash Borer Beetles (z= 7.08) , and less Golden Nematodes ( z = -7.76) , than there are in the predictive model for the county.  

3. Comparing the size of all parties that attended a park in the year 1960, and sample group of 25 parties in 1985, we are trying to see if there is no difference in overall group sizes between the time periods (null hypotheses) or to see if there is a difference (alternative hypotheses).  To test the null hypotheses, we compared the t scores of the sample data to the critical values associated with a one tailed test with 95% confidence level.  T scores were used for this data set because the number of observations is below 30.  The t-score of the sample data was 4.92 and the critical value derived from the 95% confidence level was 1.711.  as a result of the t score being higher then the critical value, we reject the null hypotheses.  In conclusion, these results indicate  that if you were to randomly sample an observation from both time periods, the party from 1985 would have a higher chance of having more group members.  

Part 2: Introduction

                For part two of this assignment, students are too chose three variables and compare the prevalence of said variables between southern counties and northern counties within the state of Wisconsin.  The three variables I chose to investigate (all per county) were ATV trail mileage, number of non-residential gun-deer permits, and number of non-residential 15 day fish license.  I chose these variables because Northern Wisconsin often is associated with rustic wildlife and outdoor fun, and we want to see if the patterns in human behavior and attributes of the land coincide with this idea.   The null hypotheses for this situation would be that there is no real difference in these variables between the counties in the north of the state and the counties in the south of the state.  Conversely, the alternative hypotheses is that there is a difference across the geographic space of north and south for the variables selected.  To test the null hypotheses, the data provided will be mapped to show the spatial distribution of the measured variables.  Subsequently, Chi squared tests will be used to either reject or fail reject the null hypotheses for each variable. 

Figure 2: A visual reference for how the northern counties and southern counties

relate to Highway 29

Methods

                The first step in preparing the data for further analysis is to create all the necessary layers in Arc-map.  To begin, we must join the data provided in SCORPARCGIS table provided in an excel spreadsheet, to a shape file of Wisconsin counties.  The join conducted was based off of the county field from both the counties shape file and the SCORP table,  the cardinality of this join was one-to-one and matched for all 72 counties.  The next step was to add 4 fields to the joined tabled; the first added field will delineate weather a county is north of Highway 29 (1 value) or south of Highway 29 (2 value).  The result was an even split of 36 counties in both the north and south portions. The other three fields added were used to classify my selected variables on a scale of 1,2,3,4. The higher the ranking the more of that variable is in that county.   The 1,2,3,4 ranking system was based on what category a county fell into when symbolized into a cloropleth map that was based on a natural breaks, four class classification.  Once all the values were added for all the new fields for all the counties, the next step is to create the maps and cross tab reports necessary to make conclusions about the null hypotheses.

Results

The Three maps created respectively represent the distribution of ATV trails (miles), non-resident gun-deer licenses, and non-resident 15 day fishing licenses  through the counties of the entire state of Wisconsin.  The colored categories  that you can see in in the legend, and the numbers that they are associated with are  the bases for the 4 categories that were discussed in the methods section of this report.  One of the more important thing that these maps convey to us is how for each map, the counties that represented the highest categorical value (dark green - category 4) are almost entirely in the Northern Counties for all variables.  however, other than that observation, these maps do not indicate fully if there truly is a remarkable difference between the two parts of the state.   We must must do further analyses with the Chi-Squared tests to see if their is a remarkable difference in the spatial occurrence of these variables across the north and south divide. 

After conducting the Chi-Square operation on three selected elements, the following charts were produced.  To reject the null hypotheses the Pearson Chi-Square value had to fall outside of the 9.49 critical value, which is associated with a 95% confidence level corresponding with 3 degrees of freedom.

Non- resident 15 day fish license Score =  12.0
ATV trail mileage score = 15.0
Non-resident gun-deer license score = 6.6

In regards to these results the null hypotheses is rejected for both ATV trail mileage and non-resident 15 day fish licenses.  conversely, we fail to reject the Null hypotheses for non-resident gun-deer licenses.  in the tables below, the values to pay attention too in the first box in each section are the ones in the first row. The Chi-Squared Value for each factor is already listed above, the third value when subtracted from 1 gives you the relative percentage which indicates your confidence in that there is a difference between the northern and southern counties.  The second box in each section displays the difference between the expected values, based off of random selection, and the observed values for each ranked category in the north and the south.


1.  Non-resident 15 day fish license

Score = .007



NOTE: 1 = NORTHERN COUNTIES  
              2= SOUTHERN COUNTIES 

 2.  ATV trail miles

3.  Non-resident gun- deer licenses

Conclusion

If looking for a sense of  "Up-North" is the goal, we may have found it.  I believe this based off of my results because two out of my three factors ended up showing a much stronger prevalence in the north than in the south.  Suspicions were rising when i created the map that there was a spatial difference, and running the Chi-Square test confirmed my findings that there is a difference between what is observed and what is expected.  In other words, there was something in the north that was creating the conditions for a higher occurrence of 15 day fishing licenses and more ATV trails. when comparing the maps, the fact that  there is a higher prevalence of non residential fishing licenses implies that this is where the most attractive fishing is in the state.  Attractive in the sense of the number of lakes, variety and availability of fish, and even overall surrounding.  People from out of are traveling all the way up to the Northern part of the state would imply that there is a more rustic and natural vibe 'Up-North'.  Not as convincing or telling an argument, but the higher amount of ATV trail miles indicates even more so that the Northern Counties in Wisconsin is the best destination for outdoor and recreation in the state.  Finding out that the number of non-residential deer licenses was more evenly spread out than the other factors was not to my surprise.  Unlike lakes and trails, deer and deer populations have a much higher degree of mobility, and thus are more randomly spread out. eliminating the out-liers of the northwestern counties that border Minnesota, you might even see more hunters in the south than in the north.  The chi squared values were very helpful in confirming that suspicion that was visual provided by the map, and cemented my conclusion that the physical landscape conditions are different in the northern part of the state, leading to the rejection of the null hypotheses.

Spatial Statistics: Weighted Mean Centeres and Z Scores.

Introduction

The problem presented in this project pertained to trying to decipher if their has been any geographic shift in where tornado's occur in in the states of Oklahoma and small part of Kansas.  The claim that some citizens of these states make, is that the pattern of tornado events hasn't changed geographically , therefore they shouldn't be forced to build a protective shelter if they live an area with few tornadoes.  The state governments believe that it is in the best interest that everyone should have them, simply to be safe.  To seek sense out of this situation and make a more scientific assessment, their should be a statistical analyses of the areas tornadoes by taking into consideration both the locations and magnitude across two separate but aligned time periods, over the same span of space covering parts of Kansas and Oklahoma.

Methods

The data provided incorporated an almost complete set of information that would be necessary to compare tornado patterns of location and magnitude across the state of Oklahoma and a portion of Kansas. There were three files used to run the analyses on the tornado data: two shape files containing the location and width of the tornado, one set from 1995-2006 and the other from 2007-2012. The third file was shape file of all the counties in the area of interest and also contained the count of tornadoes per county, but only for the 2007-2012 period (hence why I said 'an almost complete set of information').

The first set of analyses that was conducted was to find the weighted mean centers for each time periods.  a weighted mean centers averages out the totality of all the x and y coordinates, and divides both by the number of observations. The result is an x,y coordinate that is at the centroid of all the other points. In allocation with finding the center point of the tornado activity, another pattern that needed analyses  was magnitude.  To do this we used the weighted mean center tool in Arc Map, which does the same operation as a weighted mean center but also allows you to add another factor into the equation, in this case width.  basing the weighted mean center on width pulled the previous geographic mean center of all the tornadoes towards where there were more tornadoes that were larger, and thus more powerful.  These maps can be seen in figure 1 under results

 Another calculation that was made was made using the this data was standard distance operations.  this incorporates both a weighted mean center and adds an circular area that represents the a first order standard deviation of tornadoes occurrences.  What that circle represents is the area where a majority of the tornadoes occurred, and also where the stronger and bigger ones are occurring. These maps can be seen in figure 2 under results


 Results

Figure 2: Three maps which emphasis the mean center and weighted mean center of the Tornadoes in Oklahoma/Kansas. notice the little variance





Figure 2: The emphases of these maps are the standard distances that were applied to each time periods weighted mean center. once again notice the little variance.

County Tornado Statistics

Mean = 4
Standard Deviation = 4.3
range = 0-32



The final analytical procedure employed on this data was to analyze the standard deviation and z scores of the tornado data based on the 2007-20012 county tornado data.  The standard deviation is calculated based off of a single observations variance from the mean. as expected, a majority of the counties fall within the first standard deviation (-.5 - .5).  Similarly, there are less observations that lie outside of the standard deviation.   The calculations presented in this map show a  relatively high number of counties that are above the first standard deviation.

Using both the standard deviation and the mean, students were asked to calculate the z score for three counties.  The z score indicates the actual variance a particular observation deviates from the mean score of all counties.  Using the score of that particular observation you can then find the probability that an observation will occur, with relevance to the data of that time period. The standard deviation of all these counties, as well as the z and p scores of the specified are all illustrated in figure 3.  The percentage associated with the three counties is the probability that a tornado would not occur if the current weather patterns stay the same.

Figure 3: Map showing standard deviation of all counties while also showing the z and p scores of the specified counties.

Conclusion

The overall results that these analytical techniques provided was that between the time periods between 1995-2006 and 2007-2012 the patterns of tornadoes changed very little.  As you can see in the maps of the weighted mean centers and mean centers, the contrasting time periods showed little variation over the period of  17 years.  In regard to the standard deviation, that indicates that a majority of the counties have somewhere between 2-6 tornadoes in their county over a 5 year time period.  As the  map in figure 3 illustrates, there is not much of any pattern that can be seen throughout the area of interest in regards to where more tornadoes are occurring. In a best case scenario I would be able have the count data of tornadoes per county for the 1995-2006 time period for the sake of comparing the change of specific counties. In the 2007-2012 period, only 11% of the counties in the area had 0 tornadoes while the average of each county is 4 tornadoes. 

The implications of these result suggest that tornado patterns haven't changed very much during the the past 17 years of study. The occurrences of these tornadoes are for all intensive purposes, are seemingly very random.  This conclusion came based upon the fact that the mean center is very centrally  located.  The centrality of that point suggest that the geographic occurrences of tornadoes across the area of interest is more or less well dispersed, both in strength and number. In essence what that means is although patterns have not changed,  this model suggests that there is no guarantee of an area being safe from tornadoes.  In regards to all statistics and models calculated, I would advise people to invest in having a tornado shelter.