Regression Analysis

Part 1

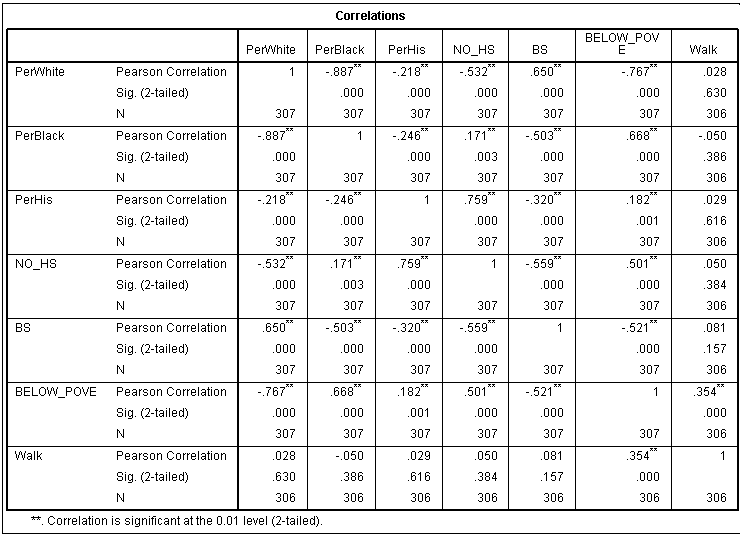
A study done on an unknown town is trying to test to the relationship between the amount of students who get free and reduced lunch and crime rates.  A news station within this town has made the claim that as the amount of kids who are receiving free lunch goes up, so does the crime rate.  Using the same 44 observations as the news station, a regression analyses will be ran to test if the percentage of persons enrolled in free lunch programs correlates too a differentiation in crime rates.  The null hypotheses in this instance would be that there is no relationship between percent of students receiving free lunch and the crime rate within Town X.

Using SPSS to run the regression analyses, the charts in figure 1 were produced.  The chart on the bottom, titled coefficients, eludes that there is some degree of linear association between the two variables based off of the significant value of .005, which falls outside of the confidence interval of .05. Also, the B value is 1.685 which indicates that the linear relationship is positive. Subsequently, the top chart, titled Model Summary, provides the R square value which describes the strength of causation between percent students receiving free lunch and crime rates.  This value provides what is known as the coefficient of determination, and in this case the value is .173.  In conclusion, we acknowledge that there is weak linear association, and therefor we reject the null hypotheses

Figure 1: charts displaying results of linear regression analyses ran in SPSS.

Using linear regression equation, what percentage of persons will get free lunch with a crime rate or 79.7?

y = a + bx

independent variable = percent free lunch
dependent variable = crime rate

a= constant  (shown in coefficients chart)
b= regression coefficient
y= 79.7%
x=?

79.7= 21.819 + 1.685 (x)
x= 34.35%


Part 2: Introduction 

Using the college enrollment data from all 72 counties in the state of Wisconsin, the University of Wisconsin state school system wants know why students chose the schools that they ultimately end up attending.  Does the overall trend show students going to schools close by? faraway? Or does the county distance from a school not matter and socio-economic factors like education and household income have more of an effect.  It must be acknowledged that there are many unknown variables which can not be accounted for in this analyses, the goal is simply to see if particular variables will display any correlating trends.  The data that we have for each county is: % population with a Bachelors degree, median house hold income, and the distance from each county's center to the different UW schools.  The schools being used to test the null hypotheses, that there is no linear relationship between distance, % population with a bachelors degree, median house hold income, and the number of people attended, are  UW Eau Claire or UW Parkside.

Methods

To find out if any of these factors are significant, a series of regression analyses were conducted to test the relationship between the number of graduates from each school per county and the factors alluded too in the intro.  A total of six linear regressions were ran, all of which had either UWEC students or UWPS graduates per county as the the constant dependent variable and pop/distance, median household income, or percent population with a Bachelors Degree as the independent variable.   Conducting linear regression indicated if any and what variables affect the amount of students from each county attend the schools in question. 

Of these six regression analyses ran, only three were found to be significant based on a one tale test with a 95% confidence interval.  So the only results that will be discussed from here forth will be those that fell outside of the 95% range, since they rejected the null hypotheses.

The linear regression that yielded significant results were:

1. population of UWEC students per county compared too population/distance
2. population of UWEC students per county compared too percent population of county with BS degree
3. population of UWPS students per county compared too population/distance

Note: population of students per school in each school was normalized by distance so the counties with large populations don't create false data.  The counties that contain the states larger cities cities likely have the most students enrolled all over the state school system, hence why the normalization of distance is necessary.

Results

1. Results of Regression analyses between population UWEC students to population/distance per County.

The linear relationship between distance and population of students per county poses very high coefficients of determination.  This not only concludes the linear nation of relationship, but it is strong enough that it can be a tool to help predict the future enrollment patterns based off of a counties distance from UWEC.  The overall pattern of the residual range suggest that the closer ones county is to the campus, the higher likelihood they will attend the UWEC. Looking at the map one can see that there is significant clustering of higher residual categories around Eau Claire County.  The other counties that exhibit high portions of UWEC studetns are those that reside on the eastern side of the state where a large portion of the states population lives.  The fact that these areas still demonstrate high residual values despite  being on the other side of the state suggest that there is a motive at play here that isnt quite as tangable or obvious.  Perhaps its showing a body of students that want to escape the big cities and see what life is like an a more rural/town environment



2. Resaults of regression analyses between population UWEC students and Percent of counties population with a BS Degree.

 When analyzing the relationship between UWEC students and percent BS degrees per county county is that there is not a very strong coefficient of determination.  Despite the fact that there is a linear relationship between the two variables, the low coefficient determination would indicate that the presence of higher or lower % BS degrees per county has little affect on the amount of students from that county that attend UWEC.  Another way this variable could be applied to show stronger relationship is to apply the same variable to the entire network of Wisconsin state schools.  This would test the assumption that a college education for ones children is more common if they come from a family or environment where a college education is more common. 

3. Results of regression analyses between population of UWPS students percounty and population/distance per county

Similar to the comparison between UW Eau Claire and distance, the comparison between UW Parkside students and population/distance per county also showed a high coefficient of determination.   The predictive value of the relationship is especially significant when one looks at the map and can clearly see that not many people attend UWPS who are not from the eastern or south eastern part of the state.   Another observation that can clearly be seen is that the highest residual degree is only associated with two counties; the county the school is in (Kenosha) and the county directly north of Kenosha County (Recine). Of all the results discussed, the findings in this analyses show the highest degree of predictive value.

Conclusion 

running regression analyses to see what factors contributed to how many people per county go to a certain school yielded some interesting results.  The main finding was that the distance between UWEC/UWPS and a given county is a huge factor in predicting where a student will go to university. Personally, i can say that this factor did way into my decision greatly, I dint want to leave too far from home, but i wanted to be far enough away where i want tempted to go home all the time.  With that being said, I'm sure many students weigh many other variables when deciding what school to attend, and some universities tend to attract more people from closer locations than others.  In light of my results, smaller schools, like UW Park-side, and to a smaller degree, UWEC, would be able to use the results of this analyses to sharpen the focus of their advertising and recruitment to the counties that immediately surround them.

Correlation and Spatial Autocorrelation Lab

Part 1: Correlation 

For the introductory portion of this lab, students ran correlation analyses on a data set to test the relationship between distance (ft) and sound level (db).  The null hypotheses in this case would be that here is no linear relationship between the distance from the source, and how strong the sound is  To test the null hypotheses,  the data was analyzed in excel and SPSS to get both the direction and strength of the relationship. The data was used in Excel to create a scatter plot with a trend line, which was used to provide the direction of the correlation.  The minimum values of the x an y values were adjusted so the data better filled out the graph area.  As the graph indicates, there is a negative correlation where as distance increases, the sound level decreases (figure 1).  The next operation was too find the strength of association between these two variables, which was done using the 'bi-variate correlation' tool in SPSS.  The resulting r value of -.896  in this operation indicates that there is a strong association between distance and sound level. As a result, we reject the Null hypotheses that there is no linear correlation.

figure 1

figure 2 

Part 2: Creating and Analyzing a Correlation Matrix.


Looking at the correlation matrix for the 307 census tracks in Milwaukee County, one can see a range of correlations pertaining to the racial demographics, education, and socio-economic factors within the county.  The trend that is displayed in these correlations paints a general picture of segregation and inequality. To exemplify this overall trend within the county, it is important to pay attention to the observable correlation between the variables presented in figure 3 below.  The first correlation that shows a degree of segregation is shown in the strong-negative correlation between percent black people/census track and percent white people/census track (-.887).  Subsequently, there is a strong positive correlation between percent black people/census track and percent below poverty level/ track (.668).  When looking at the same comparison for white people though, you see the opposite trend of a strong negative correlation correlation (-.767).   These three correlations previously commented on indicate that on track to track basis, that if there is a high percent of white people in the track, there is a high probability of there being a low percentage of black people and a low percentage of people below the poverty line.

figure 3

Part 3: Spatial Autocorrelation - Introduction 

For this section, the TEC is asking to find any patterns in voting demographics for elections that occurred in 1980 within the state of Texas.  The data you have been given for these two election periods is the overall voter turnout and the percent of the democratic vote, per county.  subsequent to this electoral data, data was also downloaded that contained the total population of Hispanics per Texas County in 2010.  The goal is to report back if voting patterns have changed in the past 20 years; and if so, how?  The null hypotheses that we are testing is if there is no change in voting patterns between 1980 and 2008, and the alternative hypotheses being that there is a difference between in voting trends between these two years.


Methods

Spatial Auto correlation is a tool that is used if one is trying to see how a single variable changes over a given area if the data is in a continuous format.  Following Tobler's first law of geography, that things closer together are more related and interconnected than things further away, spatial auto correlation than allows one to create a much more useful concise statistical picture of how a variable undergoes variation over a given space.  Most other statistical methods are based on the assumption that the values of observations in each observation, occur independent of one another. Spatial autocorreltaion allows you to see what areas show clusters where there are significantly high values of your variable, clusters of significantly low, and areas where there are hi values surrounded by low, or low values surrounded by hi.


The value used to measure of the degree of autocorrelation in this study is Moran's I.  Moran's I is applied to the zones or point where the autocorrelation is being conducted, and provides you with a number between -1 to 1.  The closer Moran's I is to 1, the more clustered the the the data is.  The direction (+/-) tells you if there is clustering (+) or if there isn't (-).

To visually comprehend how the spatial distribution of Hispanic populations and democratic voters, LISA auto-correlation maps were created to show areas of Texas where clustering is occurring, where it is not, and where out-lier counties are.  In order to create these maps, a spatial weight must be created within Opengeoda.  The spatial weight that was created was based off of shared border length. as a result,   Larger counties which had more a large boarder perimeter, and a large amount of smaller counties around it were given a heavier weight than smaller counties.  This addition of a spatial weight to the auto correlation provides a spatial element that helps create areas of clustered similarities.

To produce these values and maps, all data and weights were created/inputted into in OpenGeoda, a free interface for geo-statistical analyses. the correlation matrix produced was created in SPSS.



Results and Subsequent Conclusions 

• High - High = counties that show a high level of the variable, and are surrounded by other counties which exhibit high levels of the variable 
• Low-Low = counties that show a low level of the variable and are surrounded by other counties which exhibit low levels of the variable 
• Low - High = counties that exhibit a low level of the variable but are near areas that show a high level of the variable 
• High - Low = counties that show high levels of variables but are near areas that show low levels of the variable

Percent of population of Hispanics per County in Texas, 2010

This map illustrates the highest degree of spatial autocorrelation out of all the observations.   Along the border with mexico, there is distinctly visible high-high clustering, and a high degree of low-low clustering in the Eastern part of the state.  besides a select few high-low or low-high outliers, The general trend suggests that Hispanic populations are more concentrated near the Mexican border in the south/south western part of the state, and moves toward low-low levels of clustering as you move north and east. In addition to the visual prevalence of the clustering, the subsequent Moran's I of .78 further suggest a high degree of positive autocorrelation.



Percent Democratic voter turnout (2008 top - 1980 bottom)

Between the years of 1980 and 2008, the voting pattern of percent democratic voters become more clustered and less random.  where there was once counties of 'high-high' democratic vote percentage in 1980, there isn't in in 2008.   The maps would suggest that for some reason the democratic vote shifted from pockets in the south/south east to being more concentrated near the border areas in the south/south west, and a small part of the north east.  Subsequently, the Moran's I value increased between these two years from 0.58 to .7, further indicating that a higher degree of clustering is occurring of percent democratic vote turnout per for each county in Texas.


Voter turnout (2008 top - 1980 bottom) 



































Unlike the spatial auto correlation conducted on percent democratic vote between the two years 1980 and 2008, the spatial auto correlation of overall voter turnout between 1980 and 2008 showed a decrease in the amount of clustering; the Moran's I score drooped from .46 in 1980 to .36 in 2008.  The clustering that is still occurring, however, has shifted from the south west of the state up toward the middle, north and north eastern parts of the state.  Subsequently the, southern tip of the state that was almost entirely high-high, is now entirely low-low.  The reason for this switch could be any number of factors; growth of population in new areas, the decrease of population in other areas.


To further investigate if there are any correlations between the variables that occurred in the same year (2008), a correlation matrix was produced in SPSS.  Since it would make no sense to analyze the correlation of things that occurred 28 years apart, the correlation focused on the comparing percent Hispanic population per county, and the 2008 % democratic vote and overall voter turn out per county.  what can be seen is a moderately strong negative correlation between % Hispanic population and voter turnout but see a moderate strong correlation between % Hispanic population and % democratic turnout. The later observation indicates that as the % of democratic voters increases through out the state, there is a significant probability that you will find a higher % of a counties population being Hispanic.  Transversely, the moderately strong negative correlation between % Hispanic population and overall voter turnout suggests a higher probability of counties that have a low voter turnout also having a high percentage of the population being Hispanic.

Report to the TEC 

In conclusion to the reports and maps created, the Null hypotheses would be rejected in this scenario because a large spatial shift in voter turnout and % democratic vote can be observed across counties within the state of Texas between 1980 and 2008. Reporting to the Governor, the findings from this report would suggest that the spatial distribution of voting patterns have changed from 1980 to 2008.  The southern part of the state which in 1980 exhibited an area with a predominantly low voter turnout made a complete change to 2008, and became an area of high voter turnout.  one possible reasoning for this could be related to the high Hispanic population that we now see there in the 2010 data.  With more time and resources, analyzing the Hispanic populations within the state around the time of the 1980 election would allow for a more in depth analyses of the possible influence of Hispanic population on the overall voter turn out within the state of Texas.  In terms of the % democratic vote, the shift of clustering toward the southwestern part of the state coincides well with the % Hispanic population clustering exhibited in 2010.  At this point in time, Hispanics largely vote democratic, so this trend isn't particularly alarming. The governor now should be better able to comprise a plan of action of where to focus his campaign  efforts to reach the parts of the state with the highest voter turnout and while also targeting clusters of Hispanic populations.